Drone Programming - How to Program your Drone to Fly in a Square Trajectory using DroneKit-Python?
December 28, 2021 in Aerospace, Programming by ![]() Dhulkarnayn—12 minutes
Dhulkarnayn—12 minutes
Embarking on the journey of programming a drone might seem daunting at first, but fear not – it’s more accessible than you might think. The expanding applications of drones across diverse industries underscore their growing significance. Dive into the realm of drone programming with a plethora of resources and guides available online, supporting multiple programming languages such as C, C++, Python, and more.
Drone programming extends beyond the realm of mere autonomous takeoff and landings. There are instances where drones are tasked with specific missions tailored to meet your requirements or those of your customers.
Video Credits: Dhulkarnayn, Elucidate Drones
Imagine wanting to program your drone to gracefully trace a triangular or square trajectory through the skies. The first step? Delve into the mathematical intricacies behind this aerial choreography before translating it into code.
As drones soar through the skies, relying heavily on the Global Position System (GPS) for outdoor navigation, it’s crucial to acknowledge the substantial mathematical groundwork underpinning their guidance and navigation. Brace yourself for an adventure where algorithms and coordinates dance in harmony with the crisp, open air.
A Guide to Program Your Drone for a Dazzling Square Trajectory
Embarking on the thrilling adventure of programming your drone to gracefully trace a square trajectory requires a rendezvous with the geometry of the square itself. Picture a square – a captivating regular quadrilateral, boasting four sides of equal length and four angles of perfect symmetry.
Image Credits: Dhulkarnayn, Elucidate Drones
Explore the fascinating characteristics of a square, where every angle stands at attention, measuring a perfect 90°. Each side of the square proudly matches its counterparts in length, with opposing sides running parallel, akin to a symphony of geometric precision. As if choreographed, the diagonals intersect at a harmonious 90°.1
Note
The magic behind the scenes lies in the python script employed in this article, crafted with an intricate understanding of the geometric poetry of a square.
Now, the exhilarating journey commences. Your initial task involves sculpting a path that embodies the essence of a square, transmuting its local coordinates into the captivating tapestry of geographical coordinates – latitudes and longitudes. Once the stage is set with these geographic notes, it’s time to orchestrate the drone’s flight, guiding it gracefully from point to point in a seamless dance.
Immerse yourself in the symmetrical dance of angles, where every corner echoes with the melody of 90°. Armed with the side length in meters, envision the calculation of the next geographic point – a process as elegant as incrementing the angle to 90° from the current heading of the drone.
Repeat this balletic maneuver four times, and voilà! The airspace is now painted with the enchanting trajectory of a square, a spectacle born from the fusion of mathematical precision and airborne finesse.
Dive into the Square Mission Script with DroneKit-Python Magic
Embark on a thrilling coding adventure as we unveil the mystical script orchestrating the square mission using DroneKit-Python. To join this coding escapade, simply summon the script to your device with the following git command:
git clone https://github.com/Dhulkarnayn/square-mission-dronekit-pythonNote
For those not acquainted with the magical powers of git, fear not! Conjure it into existence on your device by reciting the following commands in your terminal:
sudo apt-get update
sudo apt-get install gitAlternatively, if you prefer the art of copy and paste, inscribe the following incantations into a file named square_mission.py on your device. Let the coding symphony begin!
The Script
1#!/usr/bin/env python
2
3#..................................................................................
4# Author : Saiffullah Sabir Mohamed
5# Github : https://github.com/TechnicalVillager
6# Website : http://technicalvillager.github.io/
7# Source : https://github.com/TechnicalVillager/square-mission-dronekit-python/
8#..................................................................................
9
10# Import Necessary Packages
11from dronekit import connect, VehicleMode, LocationGlobalRelative
12import time, math
13
14def basic_takeoff(altitude):
15
16 """
17
18 This function take-off the vehicle from the ground to the desired
19 altitude by using dronekit's simple_takeoff() function.
20
21 Inputs:
22 1. altitude - TakeOff Altitude
23
24 """
25
26 vehicle.mode = VehicleMode("GUIDED")
27 vehicle.armed = True
28 time.sleep(2)
29 vehicle.simple_takeoff(altitude)
30
31 while True:
32 print("Reached Height = ", vehicle.location.global_relative_frame.alt)
33
34 if vehicle.location.global_relative_frame.alt >= (altitude - 1.5):
35 break
36
37def change_mode(mode):
38
39 """
40
41 This function will change the mode of the Vehicle.
42
43 Inputs:
44 1. mode - Vehicle's Mode
45
46 """
47
48 vehicle.mode = VehicleMode(mode)
49
50def send_to(latitude, longitude, altitude):
51
52 """
53
54 This function will send the drone to desired location, when the
55 vehicle is in GUIDED mode.
56
57 Inputs:
58 1. latitude - Destination location's Latitude
59 2. longitude - Destination location's Longitude
60 3. altitude - Vehicle's flight Altitude
61
62 """
63
64 if vehicle.mode.name == "GUIDED":
65 location = LocationGlobalRelative(latitude, longitude, float(altitude))
66 vehicle.simple_goto(location)
67 time.sleep(1)
68
69def change_alt(step):
70
71 """
72
73 This function will increase or decrease the altitude
74 of the vehicle based on the input.
75
76 Inputs:
77 1. step - Increase 5 meters of altitude from
78 current altitude when INC is passed as argument.
79
80 - Decrease 5 meters of altitude from
81 current altitude when DEC is passed as argument.
82
83 """
84
85 actual_altitude = int(vehicle.location.global_relative_frame.alt)
86 changed_altitude = [(actual_altitude + 5), (actual_altitude - 5)]
87
88 if step == "INC":
89 if changed_altitude[0] <= 50:
90 send_to(vehicle.location.global_frame.lat, vehicle.location.global_frame.lon, changed_altitude[0])
91 else:
92 print("Vehicle Reached Maximum Altitude!!!")
93
94 if step == "DEC":
95 if changed_altitude[1] >= 5:
96 send_to(vehicle.location.global_frame.lat, vehicle.location.global_frame.lon, changed_altitude[1])
97 else:
98 print("Vehicle Reached Minimum Altitude!!!")
99
100def distance_calculation(homeLattitude, homeLongitude, destinationLattitude, destinationLongitude):
101
102 """
103
104 This function returns the distance between two geographiclocations using
105 the haversine formula.
106
107 Inputs:
108 1. homeLattitude - Home or Current Location's Latitude
109 2. homeLongitude - Home or Current Location's Longitude
110 3. destinationLattitude - Destination Location's Latitude
111 4. destinationLongitude - Destination Location's Longitude
112
113 """
114
115 # Radius of earth in metres
116 R = 6371e3
117
118 rlat1, rlon1 = homeLattitude * (math.pi/180), homeLongitude * (math.pi/180)
119 rlat2, rlon2 = destinationLattitude * (math.pi/180), destinationLongitude * (math.pi/180)
120 dlat = (destinationLattitude - homeLattitude) * (math.pi/180)
121 dlon = (destinationLongitude - homeLongitude) * (math.pi/180)
122
123 # Haversine formula to find distance
124 a = (math.sin(dlat/2) * math.sin(dlat/2)) + (math.cos(rlat1) * math.cos(rlat2) * (math.sin(dlon/2) * math.sin(dlon/2)))
125 c = 2 * math.atan2(math.sqrt(a), math.sqrt(1-a))
126
127 # Distance (in meters)
128 distance = R * c
129
130 return distance
131
132def destination_location(homeLattitude, homeLongitude, distance, bearing):
133
134 """
135
136 This function returns the latitude and longitude of the
137 destination location, when distance and bearing is provided.
138
139 Inputs:
140 1. homeLattitude - Home or Current Location's Latitude
141 2. homeLongitude - Home or Current Location's Longitude
142 3. distance - Distance from the home location
143 4. bearing - Bearing angle from the home location
144
145 """
146
147 # Radius of earth in metres
148 R = 6371e3
149
150 rlat1, rlon1 = homeLattitude * (math.pi/180), homeLongitude * (math.pi/180)
151
152 d = distance
153
154 #Converting bearing to radians
155 bearing = bearing * (math.pi/180)
156
157 rlat2 = math.asin((math.sin(rlat1) * math.cos(d/R)) + (math.cos(rlat1) * math.sin(d/R) * math.cos(bearing)))
158 rlon2 = rlon1 + math.atan2((math.sin(bearing) * math.sin(d/R) * math.cos(rlat1)) , (math.cos(d/R) - (math.sin(rlat1) * math.sin(rlat2))))
159
160 #Converting to degrees
161 rlat2 = rlat2 * (180/math.pi)
162 rlon2 = rlon2 * (180/math.pi)
163
164 # Lat and Long as an Array
165 location = [rlat2, rlon2]
166
167 return location
168
169def square_calculation(side_length):
170
171 """
172
173 This function will generate the geographical coordinates (latitudes & longitudes)
174 of the square path with the given side length. The origin or reference location
175 for the generation of the square trajectory is the vehicle's current location.
176
177 Inputs:
178 1. side_length - Side length of the square
179
180 """
181
182 # Vehicle's heading and current location
183 angle = int(vehicle.heading)
184 loc = (vehicle.location.global_frame.lat, vehicle.location.global_frame.lon, vehicle.location.global_relative_frame.alt)
185
186 # Declaring a array variable to store
187 # the geogrpahical location of square points
188 final_location = []
189
190 for count in range(4):
191 new_loc = destination_location(homeLattitude = loc[0], homeLongitude = loc[1], distance = side_length, bearing = angle)
192 final_location.append((new_loc[0], new_loc[1], loc[2]))
193 loc = (new_loc[0], new_loc[1], loc[2])
194
195 # Incrementing heading angle
196 angle += 90
197
198 return final_location
199
200def square_mission(side_length):
201
202 """
203
204 This function retrieves the square coordinates from the square_calculation()
205 function and guides the vehicle to the retrieved points.
206
207 Inputs:
208 1. side_length - Side length of the square
209
210 """
211
212 # Retrieving the array of the locations of the square path
213 locations = square_calculation(side_length = side_length)
214
215 for location in locations:
216
217 # Send vehicle to the destination
218 send_to(latitude = location[0], longitude = location[1], altitude = location[2])
219
220 while True:
221
222 # Distance between the current location of the vehicle and the destination
223 distance = distance_calculation(homeLattitude = vehicle.location.global_frame.lat,
224 homeLongitude = vehicle.location.global_frame.lon,
225 destinationLattitude = location[0],
226 destinationLongitude = location[1])
227
228 if distance <= 1.8:
229 break
230
231 time.sleep(2)
232
233def main():
234
235 # Declaring Vehicle as global variable
236 global vehicle
237
238 # Connecting the Vehicle
239 vehicle = connect('udpin:127.0.0.1:14551', baud=115200)
240
241 # Setting the Heading angle constant throughout flight
242 if vehicle.parameters['WP_YAW_BEHAVIOR'] != 0:
243 vehicle.parameters['WP_YAW_BEHAVIOR'] = 0
244 print("Changed the Vehicle's WP_YAW_BEHAVIOR parameter")
245
246 while True:
247
248 # Getting Input from User
249 value = input("Enter your Input:\n").upper()
250
251 if value == 'TAKEOFF':
252 basic_takeoff(altitude = 5)
253
254 if value == 'LAND':
255 change_mode(mode = value)
256
257 if value == 'INC' or 'DEC':
258 change_alt(step = value)
259
260 if value == 'SQUARE':
261 side = int(input("Enter Side Length of the Square Path (in meters):\n"))
262 square_mission(side_length = side)
263
264if __name__ == "__main__":
265 main()Source: Link
Note
Embark on a journey to discover the mystical dance of drone yaw with the WP_YAW_BEHAVIOR parameter. This enchanted parameter holds the key to commanding the autopilot’s yaw control during missions and the Return To Launch (RTL) spell.
In our magical code realm, we’ve aligned the stars, setting the yaw behavior to 0 (Never Change Yaw). Yet, the power to alter the destiny of your drone’s dance lies in your hands. Consult the table below to decipher the meaning of each value and choreograph the perfect mission:
| Value | Meaning |
|---|---|
| 0 | Never change yaw |
| 1 | Face next waypoint |
| 2 | Face next waypoint except RTL |
| 3 | Face along GPS course |
Unleash your creativity and let your drone traverse the skies in a dance tailored to your desires! ✨🚁💃
Launching the Drone Ballet
Elevate the curtains and initiate the mesmerizing drone ballet by commanding the script square_mission.py! Unleash the magic with a single command in your terminal:
python square_mission.pyUnveiling the Aerial Masterpiece 🚁🌟
Dive into the mesmerizing spectacle of drone choreography! Witness the seamless execution of the square mission, orchestrated with precision and finesse. Behold the dance of virtual drones, gracefully gliding through the designated trajectory.
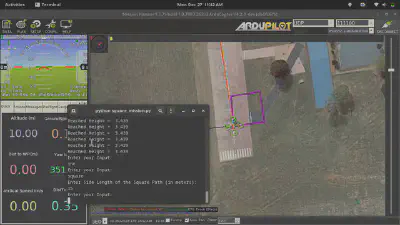
Video Credits: Dhulkarnayn, Elucidate Drones
Note
Embark on this virtual journey not with tangible drones but with the ethereal embrace of ArduPilot’s Software In The Loop (SITL) simulation. The grand spectacle unfolds within Mission Planner, a revered MAVLink supported Ground Control Station (GCS) that gracefully conducts the drone’s symphony. Whether your realm is Windows, Linux, or Mac OS, this enchanting experience awaits, thanks to the mystical essence of Mono.
Unraveling the Drone Symphony 🎮✨
Embark on an exhilarating journey of drone mastery with the square_mission.py script! This Python wizardry enables you to orchestrate any MAVLink supported drone, choreographing a graceful dance in the form of a square trajectory.
After the enchanting execution of square_mission.py, immerse yourself in the interactive realm by experimenting with the following inputs:
| Input | Description |
|---|---|
| takeoff | Takeoff |
| land | Land |
| inc | Increases the current altitude |
| dec | Decreases the current altitude |
| square | Starts the square mission |
Note
To unlock the magic, ensure you have the mystical key, dronekit, installed on your device. Utter the incantation below in your terminal if it’s not already bestowed upon you:
sudo pip install dronekitShould you encounter any mysteries during installation, seek guidance in the sacred scrolls of knowledge:
Now, let’s unveil the secrets behind the incantations in the spellbook, unraveling the essence of the core functions:
Distance Calculation - distance_calculation()
Witness the arcane powers of the distance_calculation() function! This mystical formula, rooted in the haversine tradition, unveils the secrets of distance between two sacred locations, adorned with latitude and longitude coordinates.
The incantation accepts the following parameters:
| Parameters/Arguments | Meaning |
|---|---|
| homeLattitude | Home Location’s Latitude |
| homeLongitude | Home Location’s Longitude |
| destinationLattitude | Destination Location’s Latitude |
| destinationLongitude | Destination Location’s Longitude |
Destination Location - destination_location()
Behold the mesmerizing manifestation of the destination_location() function! It summons the geographic coordinates of the destination, aligning them with the stars of the home location as its celestial reference.
The sacred parameters for this ritual are:
| Parameters/Arguments | Meaning |
|---|---|
| homeLattitude | Home Location’s Latitude |
| homeLongitude | Home Location’s Longitude |
| distance | Distance from the home location |
| bearing | Bearing angle from the home location |
Square Calculation - square_calculation()
Enter the realm of geometric sorcery with the square_calculation() function! This incantation crafts the sacred coordinates of the square’s trajectory, weaving the dance of vertices with the bestowed side length.
The magic unfolds in a loop of four iterations, invoking the destination_location() function with a change in bearing angle to 90°. The result? The formation of a celestial square trajectory.
Glimpse the arcane script in action, where the vehicle’s location and the square’s vertices unfold like an ancient tapestry.
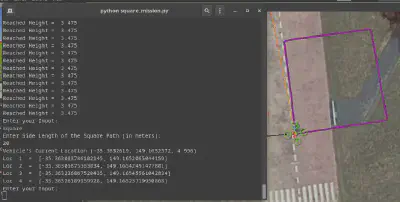
Image Credits: Dhulkarnayn, Elucidate Drones
Square Mission - square_mission()
As the climax approaches, the square_mission() function takes center stage! It beckons forth the array of sacred locations from the square_calculation() ritual, guiding the vehicle in a mystical pilgrimage through each consecrated point.
The enchanting while loop diligently monitors the distance between the vehicle and the next location, weaving the final threads of the ethereal square dance until the distance gracefully converges to zero.
Conclusion
As we wrap up this journey into the world of drone programming and the art of orchestrating a graceful square trajectory using dronekit-python, I’m thrilled to have been your guide through the skies of technology.
But, hey, the adventure doesn’t end here! Your thoughts, ideas, and feedback are the secret ingredients that make this drone odyssey truly remarkable. Let your voice soar in the comments below, and let’s spark a conversation that takes flight!
Remember, sharing the thrill of mastering drone programming is a gift that keeps on giving. So, if you found this article to be your compass in the vast skies of knowledge, why not share the joy with your friends? After all, sharing is caring, and together, we can inspire the next generation of drone enthusiasts.
Thank you for joining me on this aerial expedition.
This post is licensed under Creative Commons Attribution-ShareAlike 4.0 International (CC BY-SA 4.0) by the author.
Please consider supporting this project!
If this article has been of help to you, and you feel generous at the moment, don’t hesitate to buy us a coffee. It's an easy, fun and direct way to show your support — any amount of coffee is highly appreciated.
