Drone Programming - How to Program your Drone to Fly in a Triangular Path using DroneKit-Python?
January 9, 2022 in Aerospace, Programming by ![]() Dhulkarnayn—14 minutes
Dhulkarnayn—14 minutes
Embarking on the journey of programming a drone might seem daunting at first, but fear not – it’s more accessible than you might think. The expanding applications of drones across diverse industries underscore their growing significance. Dive into the realm of drone programming with a plethora of resources and guides available online, supporting multiple programming languages such as C, C++, Python, and more.
Drone programming extends beyond the realm of mere autonomous takeoff and landings. There are instances where drones are tasked with specific missions tailored to meet your requirements or those of your customers.
Video Credits: Dhulkarnayn, Elucidate Drones
Imagine wanting to program your drone to gracefully trace a triangular or square trajectory through the skies. The first step? Delve into the mathematical intricacies behind this aerial choreography before translating it into code.
As drones soar through the skies, relying heavily on the Global Position System (GPS) for outdoor navigation, it’s crucial to acknowledge the substantial mathematical groundwork underpinning their guidance and navigation. Brace yourself for an adventure where algorithms and coordinates dance in harmony with the crisp, open air.
Embark on the Journey: Programming Your Drone for a Triangular Flight!
Are you ready to infuse your drone with the artistry of flight, guiding it through the skies in a mesmerizing triangular path? Let’s embark on this thrilling adventure by unlocking the secrets of equilateral triangles and transforming geometric elegance into code!
Image Credits: Dhulkarnayn, Elucidate Drones
Unveiling the Magic of Equilateral Triangles
To choreograph your drone’s dance in the sky, first, let’s unravel the enchanting properties of an equilateral triangle1:
- Every side of an equilateral triangle boasts the same length, creating a harmonious symmetry.
- The interior angles, forming a perfect
60°each, infuse the triangle with a sense of balance and precision. - Altitudes, angle bisectors, perpendicular bisectors, and medians to each side all converge in a mystical coincidence.
Exploring the Dance of Angles: Interior and Exterior Unveiled
Behold the dance of angles! The exterior angle of a triangle, gracefully formed between a side and its extended companion, holds the key to our drone’s celestial journey.
Image Credits: Dhulkarnayn, Elucidate Drones
As we uncover the mystical relationship between interior and exterior angles2:
Interior angle + Exterior angle = 180°
From this celestial equation, the exterior angle is revealed through a mesmerizing calculation:
Exterior angle = 180° - Interior angle
In the realm of equilateral triangles, where interior angles gracefully measure 60°, the exterior angle emerges as a majestic 120°.
Exterior angle = 120°
Note
As we embark on the journey of triangular path calculation, the dance between exterior angles and side length unfolds, guiding our drone through the skies.
Are you intrigued? Let’s dive deeper into the code, where mathematical elegance transforms into the ethereal flight of your drone!
Embark on a Drone’s Dance: Unleashing a Triangular Flight
Ready to witness your drone gracefully carving through the skies in a captivating triangular path? Let’s dive into the enchanting process of programming it to embark on this mesmerizing journey.
Crafting the Triangular Trajectory: A Geometric Symphony
Before we delve into the intricacies of code, the first magical step involves generating a triangular trajectory and transforming its local coordinates into the captivating tapestry of geographical coordinates—latitudes and longitudes. Imagine the vertices of an equilateral triangle dancing in harmony with a chosen reference point or origin.
There are myriad ways to conjure this triangular path, but here’s a simple incantation: calculate the next geographic location by embracing the exterior angle (120°) as the bearing angle and infusing it with the magic of distance equivalent to the side length.
Repeat this spell three times, and behold—the geographic locations of your triangular trajectory are unveiled.
Guiding the Drone: A Sequential Symphony
Now that you hold the mystical coordinates in your hands, guiding your drone through its celestial dance becomes a seamless endeavor. Simply orchestrate its journey to these sequentially revealed locations, and watch the skies become a canvas for your drone’s triangular masterpiece.
Are you ready to breathe life into this geometric ballet? Let’s infuse your code with the magic of flight!
Embark on a Python Adventure: Triangular Mission with DroneKit-Python
Ready to breathe life into your drone with a captivating triangular mission? Let the magic unfold by bringing the following spell to your device. Simply execute the mystical git command in your terminal to download (clone) the script:
git clone https://github.com/Dhulkarnayn/triangular-mission-dronekit-pythonNote
For those not acquainted with the magical powers of git, fear not! Conjure it into existence on your device by reciting the following commands in your terminal:
sudo apt-get update
sudo apt-get install gitAlternatively, if you prefer the ancient art of copy and paste, inscribe the following script onto a file named triangular_mission.py on your device. Get ready to embark on a Python-powered drone journey like never before!
The Script
1#!/usr/bin/env python
2
3#..................................................................................
4# Author : Saiffullah Sabir Mohamed
5# Github : https://github.com/TechnicalVillager
6# Website : http://technicalvillager.github.io/
7# Source : https://github.com/TechnicalVillager/triangular-mission-dronekit-python/
8#..................................................................................
9
10# Import Necessary Packages
11from dronekit import connect, VehicleMode, LocationGlobalRelative
12import time, math
13
14def basic_takeoff(altitude):
15
16 """
17
18 This function take-off the vehicle from the ground to the desired
19 altitude by using dronekit's simple_takeoff() function.
20
21 Inputs:
22 1. altitude - TakeOff Altitude
23
24 """
25
26 vehicle.mode = VehicleMode("GUIDED")
27 vehicle.armed = True
28 time.sleep(2)
29 vehicle.simple_takeoff(altitude)
30
31 while True:
32 print("Reached Height = ", vehicle.location.global_relative_frame.alt)
33
34 if vehicle.location.global_relative_frame.alt >= (altitude - 1.5):
35 break
36
37def change_mode(mode):
38
39 """
40
41 This function will change the mode of the Vehicle.
42
43 Inputs:
44 1. mode - Vehicle's Mode
45
46 """
47
48 vehicle.mode = VehicleMode(mode)
49
50def send_to(latitude, longitude, altitude):
51
52 """
53
54 This function will send the drone to desired location, when the
55 vehicle is in GUIDED mode.
56
57 Inputs:
58 1. latitude - Destination location's Latitude
59 2. longitude - Destination location's Longitude
60 3. altitude - Vehicle's flight Altitude
61
62 """
63
64 if vehicle.mode.name == "GUIDED":
65 location = LocationGlobalRelative(latitude, longitude, float(altitude))
66 vehicle.simple_goto(location)
67 time.sleep(1)
68
69def change_alt(step):
70
71 """
72
73 This function will increase or decrease the altitude
74 of the vehicle based on the input.
75
76 Inputs:
77 1. step - Increase 5 meters of altitude from
78 current altitude when INC is passed as argument.
79
80 - Decrease 5 meters of altitude from
81 current altitude when DEC is passed as argument.
82
83 """
84
85 actual_altitude = int(vehicle.location.global_relative_frame.alt)
86 changed_altitude = [(actual_altitude + 5), (actual_altitude - 5)]
87
88 if step == "INC":
89 if changed_altitude[0] <= 50:
90 send_to(vehicle.location.global_frame.lat, vehicle.location.global_frame.lon, changed_altitude[0])
91 else:
92 print("Vehicle Reached Maximum Altitude!!!")
93
94 if step == "DEC":
95 if changed_altitude[1] >= 5:
96 send_to(vehicle.location.global_frame.lat, vehicle.location.global_frame.lon, changed_altitude[1])
97 else:
98 print("Vehicle Reached Minimum Altitude!!!")
99
100def distance_calculation(homeLattitude, homeLongitude, destinationLattitude, destinationLongitude):
101
102 """
103
104 This function returns the distance between two geographiclocations using
105 the haversine formula.
106
107 Inputs:
108 1. homeLattitude - Home or Current Location's Latitude
109 2. homeLongitude - Home or Current Location's Longitude
110 3. destinationLattitude - Destination Location's Latitude
111 4. destinationLongitude - Destination Location's Longitude
112
113 """
114
115 # Radius of earth in metres
116 R = 6371e3
117
118 rlat1, rlon1 = homeLattitude * (math.pi/180), homeLongitude * (math.pi/180)
119 rlat2, rlon2 = destinationLattitude * (math.pi/180), destinationLongitude * (math.pi/180)
120 dlat = (destinationLattitude - homeLattitude) * (math.pi/180)
121 dlon = (destinationLongitude - homeLongitude) * (math.pi/180)
122
123 # Haversine formula to find distance
124 a = (math.sin(dlat/2) * math.sin(dlat/2)) + (math.cos(rlat1) * math.cos(rlat2) * (math.sin(dlon/2) * math.sin(dlon/2)))
125 c = 2 * math.atan2(math.sqrt(a), math.sqrt(1-a))
126
127 # Distance (in meters)
128 distance = R * c
129
130 return distance
131
132def destination_location(homeLattitude, homeLongitude, distance, bearing):
133
134 """
135
136 This function returns the latitude and longitude of the
137 destination location, when distance and bearing is provided.
138
139 Inputs:
140 1. homeLattitude - Home or Current Location's Latitude
141 2. homeLongitude - Home or Current Location's Longitude
142 3. distance - Distance from the home location
143 4. bearing - Bearing angle from the home location
144
145 """
146
147 # Radius of earth in metres
148 R = 6371e3
149
150 rlat1, rlon1 = homeLattitude * (math.pi/180), homeLongitude * (math.pi/180)
151
152 d = distance
153
154 #Converting bearing to radians
155 bearing = bearing * (math.pi/180)
156
157 rlat2 = math.asin((math.sin(rlat1) * math.cos(d/R)) + (math.cos(rlat1) * math.sin(d/R) * math.cos(bearing)))
158 rlon2 = rlon1 + math.atan2((math.sin(bearing) * math.sin(d/R) * math.cos(rlat1)) , (math.cos(d/R) - (math.sin(rlat1) * math.sin(rlat2))))
159
160 #Converting to degrees
161 rlat2 = rlat2 * (180/math.pi)
162 rlon2 = rlon2 * (180/math.pi)
163
164 # Lat and Long as an Array
165 location = [rlat2, rlon2]
166
167 return location
168
169def triangle_calculation(side_length):
170
171 """
172
173 This function will generate the geographical coordinates (latitudes & longitudes)
174 of the triangular (Equilateral Triangle) path with the given side length. The origin or
175 reference location for the generation of the triangular trajectory is the vehicle's current location.
176
177 Inputs:
178 1. side_length - Side length of the Equilateral Triangle
179
180 """
181
182 # Vehicle's heading and current location
183 angle = int(vehicle.heading)
184 loc = (vehicle.location.global_frame.lat, vehicle.location.global_frame.lon, vehicle.location.global_relative_frame.alt)
185
186 # Offset Angle
187 offset_angle = 90
188
189 # Decrementing offset angle in the vehicle's heading angle to form the
190 # triangle direction with respect to the vehicle's heading angle.
191 angle -= offset_angle
192
193 # Declaring a array variable to store
194 # the geogrpahical location of triangular points
195 final_location = []
196
197 for count in range(3):
198 # Incrementing heading angle
199 # Exterior angle of equilateral triangle = 120 degrees
200 angle += 120
201
202 new_loc = destination_location(homeLattitude = loc[0], homeLongitude = loc[1], distance = side_length, bearing = angle)
203 final_location.append((new_loc[0], new_loc[1], loc[2]))
204 loc = (new_loc[0], new_loc[1], loc[2])
205
206 return final_location
207
208def triangular_mission(side_length):
209
210 """
211
212 This function retrieves the triangle coordinates from the triangle_calculation()
213 function and guides the vehicle to the retrieved points.
214
215 Inputs:
216 1. side_length - Side length of the equilateral triangle
217
218 """
219
220 # Retrieving the array of the locations of the triangular path
221 locations = triangle_calculation(side_length = side_length)
222
223 for location in locations:
224
225 # Send vehicle to the destination
226 send_to(latitude = location[0], longitude = location[1], altitude = location[2])
227
228 while True:
229
230 # Distance between the current location of the vehicle and the destination
231 distance = distance_calculation(homeLattitude = vehicle.location.global_frame.lat,
232 homeLongitude = vehicle.location.global_frame.lon,
233 destinationLattitude = location[0],
234 destinationLongitude = location[1])
235
236 if distance <= 1.8:
237 break
238
239 time.sleep(2)
240
241def main():
242
243 # Declaring Vehicle as global variable
244 global vehicle
245
246 # Connecting the Vehicle
247 vehicle = connect('udpin:127.0.0.1:14551', baud=115200)
248
249 # Setting the Heading angle constant throughout flight
250 if vehicle.parameters['WP_YAW_BEHAVIOR'] != 0:
251 vehicle.parameters['WP_YAW_BEHAVIOR'] = 0
252 print("Changed the Vehicle's WP_YAW_BEHAVIOR parameter")
253
254 while True:
255
256 # Getting Input from User
257 value = input("Enter your Input:\n").upper()
258
259 if value == 'TAKEOFF':
260 basic_takeoff(altitude = 5)
261
262 if value == 'LAND':
263 change_mode(mode = value)
264
265 if value == 'INC' or 'DEC':
266 change_alt(step = value)
267
268 if value == 'TRIANGLE':
269 side = int(input("Enter Side Length of the Triangular Path (in meters):\n"))
270 triangular_mission(side_length = side)
271
272if __name__ == "__main__":
273 main()Source: Link
Note
Embark on a journey to discover the mystical dance of drone yaw with the WP_YAW_BEHAVIOR parameter. This enchanted parameter holds the key to commanding the autopilot’s yaw control during missions and the Return To Launch (RTL) spell.
In our magical code realm, we’ve aligned the stars, setting the yaw behavior to 0 (Never Change Yaw). Yet, the power to alter the destiny of your drone’s dance lies in your hands. Consult the table below to decipher the meaning of each value and choreograph the perfect mission:
| Value | Meaning |
|---|---|
| 0 | Never change yaw |
| 1 | Face next waypoint |
| 2 | Face next waypoint except RTL |
| 3 | Face along GPS course |
Unleash your creativity and let your drone traverse the skies in a dance tailored to your desires! ✨🚁💃
Launching the Drone Ballet
Elevate the curtains and initiate the mesmerizing drone ballet by commanding the script triangular_mission.py! Unleash the magic with a single command in your terminal:
python triangular_mission.pyUnveiling the Aerial Masterpiece 🚁🌟
Dive into the mesmerizing spectacle of drone choreography! Witness the seamless execution of the triangular mission, orchestrated with precision and finesse. Behold the dance of virtual drones, gracefully gliding through the designated trajectory.
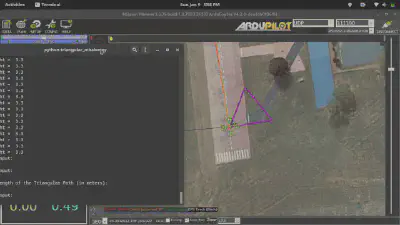
Video Credits: Dhulkarnayn, Elucidate Drones
Note
Embark on this virtual journey not with tangible drones but with the ethereal embrace of ArduPilot’s Software In The Loop (SITL) simulation. The grand spectacle unfolds within Mission Planner, a revered MAVLink supported Ground Control Station (GCS) that gracefully conducts the drone’s symphony. Whether your realm is Windows, Linux, or Mac OS, this enchanting experience awaits, thanks to the mystical essence of Mono.
Unraveling the Drone Symphony 🎮✨
Embark on an exhilarating journey of drone mastery with the triangular_mission.py script! This Python wizardry enables you to orchestrate any MAVLink supported drone, choreographing a graceful dance in the form of a triangular trajectory.
After the enchanting execution of triangular_mission.py, immerse yourself in the interactive realm by experimenting with the following inputs:
| Input | Description |
|---|---|
| takeoff | Takeoff |
| land | Land |
| inc | Increases the current altitude |
| dec | Decreases the current altitude |
| triangle | Starts the triangular mission |
Note
To unlock the magic, ensure you have the mystical key, dronekit, installed on your device. Utter the incantation below in your terminal if it’s not already bestowed upon you:
sudo pip install dronekitShould you encounter any mysteries during installation, seek guidance in the sacred scrolls of knowledge:
Now, let’s unveil the secrets behind the incantations in the spellbook, unraveling the essence of the core functions:
Distance Calculation - distance_calculation()
Witness the arcane powers of the distance_calculation() function! This mystical formula, rooted in the haversine tradition, unveils the secrets of distance between two sacred locations, adorned with latitude and longitude coordinates.
The incantation accepts the following parameters:
| Parameters/Arguments | Meaning |
|---|---|
| homeLattitude | Home Location’s Latitude |
| homeLongitude | Home Location’s Longitude |
| destinationLattitude | Destination Location’s Latitude |
| destinationLongitude | Destination Location’s Longitude |
Destination Location - destination_location()
Behold the mesmerizing manifestation of the destination_location() function! It summons the geographic coordinates of the destination, aligning them with the stars of the home location as its celestial reference.
The sacred parameters for this ritual are:
| Parameters/Arguments | Meaning |
|---|---|
| homeLattitude | Home Location’s Latitude |
| homeLongitude | Home Location’s Longitude |
| distance | Distance from the home location |
| bearing | Bearing angle from the home location |
Triangle Calculation - triangle_calculation()
The triangle_calculation() function generates the geographical coordinates of the triangular path with the given side length. It calculates the vertices of the triangular path by considering the exterior angle as the bearing and the side length as the distance for each side.
The function achieves this by invoking the destination_location() function in a loop thrice. The resulting vertices are converted into geographical coordinates and stored in an array.
To ensure the generated path aligns with the vehicle’s heading, a 90° offset is decremented from the original heading angle. This offset is crucial for preventing the path from deviating from the desired direction. True north serves as a guiding factor in this process3.
Did you know?
True north (geodetic north or geographic north) points towards Earth’s geographic North Pole.
The figure below illustrates the output with an offset value set to zero or without any offset.
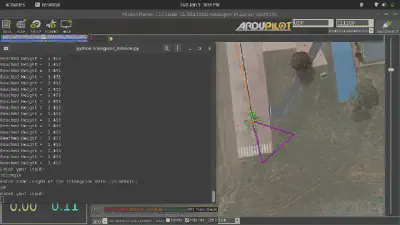
Image Credits: Dhulkarnayn, Elucidate Drones
Triangular Mission - triangular_mission()
The triangular_mission() function takes the array of locations generated by the triangle_calculation() function and guides the vehicle to each location sequentially.
The while loop in this function continuously checks the distance between the vehicle’s current location and the next location until the distance is approximately zero.
Conclusion
As we wrap up this journey into the world of drone programming and the art of orchestrating a graceful triangular trajectory using dronekit-python, I’m thrilled to have been your guide through the skies of technology.
But, hey, the adventure doesn’t end here! Your thoughts, ideas, and feedback are the secret ingredients that make this drone odyssey truly remarkable. Let your voice soar in the comments below, and let’s spark a conversation that takes flight!
Remember, sharing the thrill of mastering drone programming is a gift that keeps on giving. So, if you found this article to be your compass in the vast skies of knowledge, why not share the joy with your friends? After all, sharing is caring, and together, we can inspire the next generation of drone enthusiasts.
Thank you for joining me on this aerial expedition.
Equilateral triangle, Wikipedia. ↩︎
Sum of Exterior Angles of Triangle, Cuemath. ↩︎
True North, Wikipedia. ↩︎
This post is licensed under Creative Commons Attribution-ShareAlike 4.0 International (CC BY-SA 4.0) by the author.
Please consider supporting this project!
If this article has been of help to you, and you feel generous at the moment, don’t hesitate to buy us a coffee. It's an easy, fun and direct way to show your support — any amount of coffee is highly appreciated.

