Drone Programming - Distance and Bearing calculation between two geo-locations using python
March 8, 2021 in Aerospace, Programming by ![]() Dhulkarnayn—4 minutes
Dhulkarnayn—4 minutes
Navigation Systems, including the Global Positioning System (GPS), are crucial for both Manned and Unmanned Aircraft Systems. In GPS, positional data is represented in Geographic Coordinates System (Latitudes and Longitudes). Navigating between two points on the Earth’s spherical surface can be complex, and this complexity is addressed using the haversine formula.
Image Credits: People illustrations by Storyset
The Haversine Formula
The haversine formula, an essential equation in navigation, calculates great-circle distances between two points on a sphere based on their latitudes and longitudes.
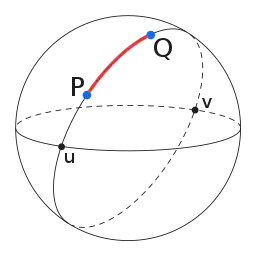
Image Credits: CheCheDaWaff, CC BY-SA 4.0, via Wikimedia Commons
The diagram above depicts the great-circle distance (highlighted in red) between two points on a sphere, namely P and Q. Additionally, the illustration includes two antipodal points, denoted as u and v.
Note
If you’re interested in delving deeper into the Haversine formula and understanding its formulation, you can explore the Wikipedia page dedicated to it. The page provides detailed insights into the formula and introduces the Law of Haversines:
This valuable resource can enhance your understanding of the mathematical principles behind the Haversine formula and its significance in navigation calculations.
Program: Distance and bearing between two geographic locations
Below mentioned code is a simple python program named distance_bearing.py that returns the distance using haversine formula and the bearing angle between two geographic locations,
1# Importing necessary Packages
2import math
3
4#Radius of earth in metres
5R = 6371e3
6
7def distance_bearing(homeLatitude, homeLongitude, destinationLatitude, destinationLongitude):
8
9 """
10 Simple function which returns the distance and bearing between two geographic location
11
12 Inputs:
13 1. homeLatitude - Latitude of home location
14 2. homeLongitude - Longitude of home location
15 3. destinationLatitude - Latitude of Destination
16 4. destinationLongitude - Longitude of Destination
17
18 Outputs:
19 1. [Distance, Bearing] - Distance (in metres) and Bearing angle (in degrees)
20 between home and destination
21
22 Source:
23 https://github.com/TechnicalVillager/distance-bearing-calculation
24 """
25
26 rlat1 = homeLatitude * (math.pi/180)
27 rlat2 = destinationLatitude * (math.pi/180)
28 rlon1 = homeLongitude * (math.pi/180)
29 rlon2 = destinationLongitude * (math.pi/180)
30 dlat = (destinationLatitude - homeLatitude) * (math.pi/180)
31 dlon = (destinationLongitude - homeLongitude) * (math.pi/180)
32
33 # Haversine formula to find distance
34 a = (math.sin(dlat/2) * math.sin(dlat/2)) + (math.cos(rlat1) * math.cos(rlat2) * (math.sin(dlon/2) * math.sin(dlon/2)))
35 c = 2 * math.atan2(math.sqrt(a), math.sqrt(1-a))
36
37 # Distance in metres
38 distance = R * c
39
40 # Formula for bearing
41 y = math.sin(rlon2 - rlon1) * math.cos(rlat2)
42 x = math.cos(rlat1) * math.sin(rlat2) - math.sin(rlat1) * math.cos(rlat2) * math.cos(rlon2 - rlon1)
43
44 # Bearing in radians
45 bearing = math.atan2(y, x)
46 bearingDegrees = bearing * (180/math.pi)
47 out = [distance, bearingDegrees]
48
49 return out
50
51def main():
52 # Initializing an Empty Array
53 dist_brng = []
54
55 # Getting inputs from the user
56 print ("+++++++++++++ Please Enter the values in decimals +++++++++++++")
57 print ("Enter the Latitude of Current location: ")
58 lat1 = float(input())
59 print ("Enter the Longitude of Current location: ")
60 lon1 = float(input())
61 print ("Enter the Latitude of Destination: ")
62 lat2 = float(input())
63 print ("Enter the Longitude of Destination: ")
64 lon2 = float(input())
65
66 # Caluculating the Distance and Bearing
67 dist_brng = distance_bearing(lat1, lon1, lat2, lon2)
68
69 # Displaying the Calculated Distance and Bearing
70 print ('Distance between the home and destination is ', dist_brng[0], ' m')
71 print ('Bearing angle between home and destination is ', dist_brng[1], 'degree')
72
73if __name__ == "__main__":
74 main()Source: Link
Execution & Output
Execute the program as follows:
python distance_bearing.pyDuring execution, input the following values:
- Home Latitude
- Home Longitude
- Destination Latitude
- Destination Longitude
The output includes the calculated distance and bearing angle:
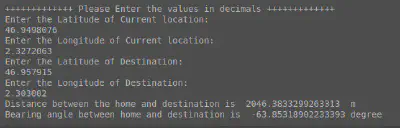
Image Credits: Dhulkarnayn, Elucidate Drones
Conclusion
Congratulations on exploring the intricacies of drone programming and understanding how to calculate distance and bearing between two geo-locations using Python! We’ve journeyed through the significance of navigation systems, the Haversine formula, and a practical Python implementation.
Now, it’s your turn! Your thoughts, questions, and suggestions are invaluable to us. What did you find most intriguing about this topic? Is there a specific aspect you’d like to explore further? Let’s keep the conversation going in the comments section below!
And remember, sharing is caring! If you’ve enjoyed this journey into drone programming, consider sharing it with your friends who might find it equally fascinating.
Thank you for being part of our exploration into the world of drone technology. Until next time, happy coding and safe flying!
This post is licensed under Creative Commons Attribution-ShareAlike 4.0 International (CC BY-SA 4.0) by the author.
Please consider supporting this project!
If this article has been of help to you, and you feel generous at the moment, don’t hesitate to buy us a coffee. It's an easy, fun and direct way to show your support — any amount of coffee is highly appreciated.